Intro
justiceHui와 Ryute가 같이 작성했습니다.
Virus Experiment (JOIOC 19 3번)
Subtask 2 (6점)
적절한 전처리를 통해 $(r, c)$가 감염되기 위해서 이웃들이 감염되어야 하는 조합을 $O(16RC)$ 시간에 모두 구할 수 있습니다. (ex. 이웃이 감염된 상태가 $\left{ N, SW, WE, SE \right}$ 중 하나 이상을 포함하면 $(r, c)$도 감염됨)
위와 같은 전처리를 모두 수행했다면, $U_{r,c} \neq 0$인 모든 $(r, c)$에 대해 BFS 등을 이용해서 시뮬레이션을 하면 $O(R^2C^2)$ 시간에 문제를 풀 수 있습니다.
Subtask 3 (100점)
깔끔한 풀이와 멋진 풀이가 있습니다. 차례대로 소개합니다.
Subtask 3 - Randomize Solution
Subtask 2는 “완전 탐색”이기 때문에 시간이 오래 걸립니다. 즉, 탐색하는 횟수를 줄이면 실행 시간도 줄일 수 있습니다. 탐색 횟수를 줄일 수 있는 방법을 생각해봅시다.
만약 “u가 감염되면 v도 감염된다”는 관계를 단방향 간선 $(u, v)$로 표현한 그래프를 만들 수 있다면, outdegree가 0인 가장 작은 SCC와 그러한 SCC의 개수가 문제의 정답이 될 것입니다. 결국 우리가 정답을 구하기 위해 찾아야 하는 것은 사이클인데, 만약 완전 탐색을 한다면 크기가 $X$인 “한 개의 사이클”을 $X$번 탐색하므로 효율적이지 않습니다. 같은 정점들로 구성된 사이클은 되도록 중복해서 탐색하는 일이 없도록 하는 방법을 찾으면 됩니다.
그 방법은 생각보다 간단합니다. Subtask 2의 풀이를 그대로 사용하되, 시작 지점이 $(r, c)$인 시뮬레이션 과정에서 $(i, j) < (r, c)$인 $(i, j)$를 방문한다면 즉시 시뮬레이션을 중단합니다. 이렇게 하면 한 사이클 전체를 다 보는 경우는 “좌표가 사전순으로 가장 작은 지점에서 시작하는 시뮬레이션” 한 번 밖에 없습니다.
하지만 이렇게 커팅을 해도 여전히 $O(R^2C^2)$가 되는 경우가 존재합니다.
이 커팅이 통하지 않는 데이터는 $(1, 1) \rightarrow (1, 2) \rightarrow (1, 3) \rightarrow \cdots \rightarrow (1, C) \rightarrow \cdots \rightarrow (1, 1)$처럼 사이클에 속한 정점의 대부분이 오름차순으로 배열된 상태일 것입니다. 이 데이터의 경우, 시뮬레이션 진행 횟수는 $C, C-1, C-2, \cdots , 1$처럼 되어서 총 수행 횟수가 제곱 스케일로 증가하게 됩니다. 기존에 비해 상수 /2가 붙긴 하겠지만요.
이것을 피하는 방법은 매우 간단합니다. 정점의 순서를 섞어주면 됩니다! 구체적으로, $U_{r,c} \neq 0$인 모든 $(r, c)$를 모아서 무작위로 섞은 순열을 $A$라고 합시다. 시작 지점이 $A_i$일 때 BFS 도중에 $j < i$인 $A_j$를 방문한다면 즉시 탐색을 중단하는 식으로 구현을 하면 위에서 본 반례를 피할 수 있습니다.
이상한 야매 풀이같지만 공식 솔루션에 나와있는 풀이입니다. 시간 복잡도는 $O(RC \log RC)$ 정도가 된다고 하던데, 증명은 안 해봤지만 아마도 여기에 나와있는 “재밌는 인터랙티브 문제”와 관련이 있을 것 같습니다.
Subtask 3 - Graph Theory
방향 그래프 $G = (V, E)$에서 SCC를 구하는 $O(\vert V \vert + \vert E \vert)$ 알고리즘은 잘 알려져 있으므로 그래프를 효율적으로 만드는 방법을 중점적으로 고민해봅시다.
추후 작성 예정…
카드 놀이 (COCI 09/10 Contest #2 6번)
Exchange Argument처럼 그리디하게 순서를 정할 수 있다는 생각이 듭니다. 카드 더미가 두 개만 있다고 가정했을 때, 어떤 카드를 먼저 써야 하는지 알아봅시다.
- 만약 맨 위에 있는 카드가 다르다면, 더 작은 카드를 사용하는 것이 이득입니다.
- 맨 위에 있는 카드가 똑같다면 사전순으로 앞서는 더미의 카드를 사용하는 것이 이득입니다. 최장 공통 접두사를 생각해보면 어렵지 않게 증명할 수 있습니다.
- 만약 어떤 카드 더미가 다른 카드 더미의 접두사가 된다면, 카드가 더 많은 카드 더미의 카드를 사용하는 것이 이득입니다.
앞글자가 제거되는 상황에서 문자열의 사전순 비교를 하는 것은 결국 모든 문자열의 suffix들을 정렬한 결과를 알고 있으면 $O(1)$에 할 수 있습니다. 이는 Suffix Array를 통해 할 수 있습니다. 모든 카드 더미를 순서대로 이어붙입시다. 그리고 나서 SA를 만들면 합친 문자열의 각 Suffix의 Prefix가 각 카드 더미의 Suffix가 되므로(말이 어렵지만 결국 우리가 비교할 때 사용하는 하나의 카드 더미의 Prefix가 합친 문자열의 Suffix에 일대일로 대응된다는 것입니다), 서로 다른 두 카드 더미의 Suffix의 대소관계를 모두 알 수 있습니다. 각 카드 더미 사이에 구분자로 매우 큰 수를 넣으면 SA의 정렬 결과를 망치지 않으면서 편하게 구현할 수 있습니다.
따라서 우선순위 큐를 이용해 모든 카드 더미 중 가장 좋은 것을 반복적으로 뽑으면서, 뽑을때마다 첫 한 글자를 제거한(바로 다음 Suffix) 카드 더미로 바꿔서 넣어주면 문제를 해결할 수 있습니다. 원소를 총 $O(\sum \vert S\vert)$번 뽑아야 하고 뽑을 때마다 $O(\log N)$ 시간이 드므로 총 시간복잡도는 Suffix Array를 계산하는 시간 $O(\vert S\vert \log \vert S\vert)$ 또는 $O(\vert S\vert \log^2 \vert S\vert)$에 $O(\vert S\vert \log N)$를 더한 만큼입니다.
별해로, 해싱을 이용해 $O(\vert S \vert)$ 전처리를 하면, $O(\log \vert S \vert)$ 시간에 비교를 할 수 있습니다. 그러므로, 우선순위 큐를 이용해 카드 더미를 관리하면 $O(\sum \vert S \vert \log^2 \sum \vert S \vert)$에 문제를 해결할 수 있습니다. 착한 어린이는 해싱을 사용하지 않고 문제를 해결해보도록 노력합시다.
Chameleon’s Love (JOISC 19/20 Day2 1번)
Subtask 2, 3 (40점)
카멜레온의 성별이 두 가지라는 점에서 이분 그래프를 생각해볼 수 있습니다. 각 카멜레온을 정점으로 생각하고, 서로 색깔이 같을 가능성이 있는 두 카멜레온을 간선으로 연결한 이분 그래프를 생각해봅시다. 두 가지 작업을 수행해야 합니다.
- 색깔이 같을 가능성이 있는 두 카멜레온을 찾는 작업
- (1)에서 찾은 후보 중 실제 정답을 구하는 작업
어떤 두 정점 $u, v$가 같은 색을 갖고 있다면 $\text{Query}(u, v) = 1$입니다. $\text{Query}(u, v) = 1$인 카멜레온을 간선으로 연결하면, 아래와 같이 각 정점의 차수가 최대 3이기 때문에 간선은 최대 $3N$개 만들어집니다. 여기까지 $2n \choose 2$번의 쿼리를 사용합니다.
- 색깔이 같은 두 정점($C_u = C_v$) 을 연결하는 간선 (각 정점마다 정확히 1개)
- 짝사랑을 하는 관계($C_u = v \lor C_v = u$)를 연결하는 간선 (각 정점마다 0개 혹은 2개)
- 만약 짝사랑을 하는 관계가 없는 경우(서로 좋아하는 경우, $C_u = v \land C_v = u$)에는 $\text{Query}(u, v) = 2$이기 때문에 정보를 얻을 수 없습니다. 따라서 간선이 만들어지지 않습니다.
만약 어떤 정점의 차수가 1이라면 매칭을 찾은 것이므로 곧바로 $\text{Answer}$를 호출하면 됩니다. 이제, 차수가 3인 정점들만 생각하면 됩니다.
차수가 3인 정점 $u$와 연결된 정점 $v$는 $C_u = C_v$, $C_u = v$, $C_v = u$ 중 정확히 하나를 만족합니다. 여기에서 $C_u = C_v$인 $v$를 바로 찾는 방법과, $C_u \neq C_v$인 $v$를 하나씩 찾아서 제거하는 방법 중 한 가지를 시도해야 합니다. 일단 $u$와 연결된 정점들에 대해서 $\text{Query}$를 호출해서 얻을 수 있는 결과를 살펴봅시다.
- $u$, $C_u = C_v$인 정점, $C_u = v$인 정점 : 2 반환
- $u$, $C_u = C_v$인 정점, $C_v = u$인 정점 : 1 반환
- $u$, $C_u = v$인 정점, $C_v = u$인 정점 : 2 반환
세 번의 쿼리 중 두 번의 쿼리는 2를 반환하고, 나머지 한 번의 쿼리는 1을 반환합니다. 그리고 1을 반환하는 쿼리에서 사용하지 않는 정점 $v$는 $C_u \neq C_v$를 만족합니다. 그러므로 “$C_u \neq C_v$인 $v$를 제거하는 전략”을 성공적으로 수행할 수 있습니다. 이 과정에서 최대 $4n$번의 쿼리를 사용합니다.
${2n \choose 2} + 4n = n(2n+3) \leq 5\,150$번의 쿼리로 문제를 해결할 수 있습니다.
Subtask 1 (4점, 총 44점)
$L_{L_i} = i$이기 때문에 모든 정점의 차수가 1입니다. $n \leq 500$이기 때문에 간선을 Naive하게 찾으면 안 되고, 조금 더 똑똑한 방법을 생각해야 합니다.
$i$번 정점을 처리하기 전에 $1 \cdots i-1$번 정점 사이에서 생기는 매칭을 모두 처리했다고 가정합시다. $i$번째 정점과 매칭할 수 있는 정점이 “아직 매칭이 안 된 정점 집합 $S$”에 존재하는지 탐색하는 방식으로 진행할 것입니다. 현재 $S$에 속한 모든 정점의 색깔이 서로 다르다는 점에 주목합시다.
만약 $\text{Query} (S + i) = \vert S \vert + 1$이라면 겹치는 색이 존재하지 않으므로 $i$번째 정점과 매칭할 수 있는 정점이 $S$에 존재하지 않습니다. $\text{Query}(S + i) < \vert S \vert + 1$인 경우를 생각해봅시다.
$\text{Query} (S) = \vert S \vert$라는 점을 이용하면 이분 탐색을 이용해서 $i$와 매칭되는 정점을 찾을 수 있습니다. 구체적으로, $S$의 원소들의 “순서”를 정한 뒤, 처음으로 $\text{Query}(S_0, S_1, \cdots , S_k, i) < k + 1$이 되는 $k$를 찾으면 됩니다.
만약 Subtask 2, 3을 먼저 풀고 오지 않고 앞에서부터 차근차근 따라 해결한다면 다음과 같은 관점으로 생각할 수 있습니다. 항상 두 카멜레온이 서로 좋아하므로, ‘좋아하는 관계’가 $\text{Query}$에 절대 영향을 주지 않습니다(항상 색이 서로 바뀌어 색의 집합은 그대로이므로). 따라서 $\text{Query}(S) = \text{Query}(S \cup x)$이면 $x$와 색이 같은 카멜레온이 $S$ 내에 존재합니다. 따라서 처음에 전체집합에서 $x$를 뺀 집합에서 시작해, 집합을 절반으로 계속 나누어가면서 색이 같은 카멜레온을 찾으면 됩니다. 이 풀이의 경우 더 간단하지만 위에서 언급한 다양한 이분 그래프의 성질을 잃어버리게 되므로, 뒤쪽 서브태스크를 해결하는 데 혼란이 있을 수 있습니다.
두 관점 모두 $O(n \log n)$번의 쿼리를 사용하므로 Subtask 1을 통과할 수 있습니다.
Subtask 4 (20점, 총 64점)
각 카멜레온의 성별을 미리 알고 있습니다. 따라서 어떤 카멜레온 $x$가 있으면, $x$가 좋아하거나, $x$를 좋아하거나, $x$와 색이 같을 수 있는 카멜레온의 집합을 미리 성별이 모두 같도록 구성할 수 있습니다.
Subtask 1의 아이디어를 살짝 빌려와, $x$와 성별이 다른 모든 카멜레온의 집합에서 이분 탐색을 수행해 봅시다. 이 집합에는 서로 좋아하는 카멜레온이나 색이 같은 카멜레온이 없으므로(간선이 존재하지 않으므로) 집합의 절반을 $T$라고 하면 $\text{Query}(T \cup x)$가 $\vert T\vert + 1$인지를 확인함으로서 $\exists p \in T$와 $x$ 사이에 간선이 존재하는지를 확인할 수 있습니다. 따라서 한 번 이분탐색을 진행할 때마다 하나의 간선을 찾아낼 수 있습니다.
각 정점에 대해 degree는 최대 3이므로 위 과정을 세 번 반복하면 모든 간선을 찾아낼 수 있습니다. 그 이후는 Subtask 3과 같이 간선으로 적당히 좋아하는 관계를 찾고 이를 바탕으로 색깔이 같은 쌍을 찾아낼 수 있습니다.
Subtask 5 (100점)
이제는 카멜레온의 성별을 모릅니다. 하지만 카멜레온들이 이분 그래프를 이룬다는 것은 알고 있기 때문에, 카멜레온의 성별을 임의로 지정하되 간선으로 이어진 카멜레온들의 성별을 다르게 유지함으로서 카멜레온의 성별을 알고 있는 것처럼 행동할 수 있습니다. 정확히는 $i$번 카멜레온을 이분 그래프에 추가할 때 $1 \dots i-1$번 카멜레온과의 간선을 찾아줌으로서 $i$번 카멜레온의 색깔을 귀납적으로 결정할 수 있습니다(결정할 수 없을 수도 있는데, 그러면 후술하겠지만 그냥 아무 색깔로 두어도 상관이 없습니다).
$1 \dots i-1$과의 간선은 어떻게 찾아야 할까요? 현재 카멜레온의 색깔을 모르므로 Subtask 4와 같이 해결하기는 힘듭니다. 그러나 카멜레온의 성별을 임의로 지정해(이분 그래프를 만들어) 유지하고 있으므로, 이분 그래프의 각 부분 자체는 Subtask 4와 같이 서로 성별이 같습니다. 따라서 두 부분에 대해 모두 Subtask 4와 같은 방법을 수행할 수 있습니다.
다만 문제는, 우리가 관리하고 있는 이분 그래프가 연결 그래프가 아닐 수 있기 때문에 두 부분에 간선이 나뉘어 들어갈 수 있다는 뜻입니다. 이로 인해 처리해주어야 하는 첫 번째 포인트는 쿼리 개수를 낭비하지 않기 위해 각 부분에 추가할 간선이 존재하는지를 미리 확인해주어야 한다는 점입니다. 두 번째 포인트는 색깔의 파괴입니다. 요약하면 아래 그림과 같습니다.
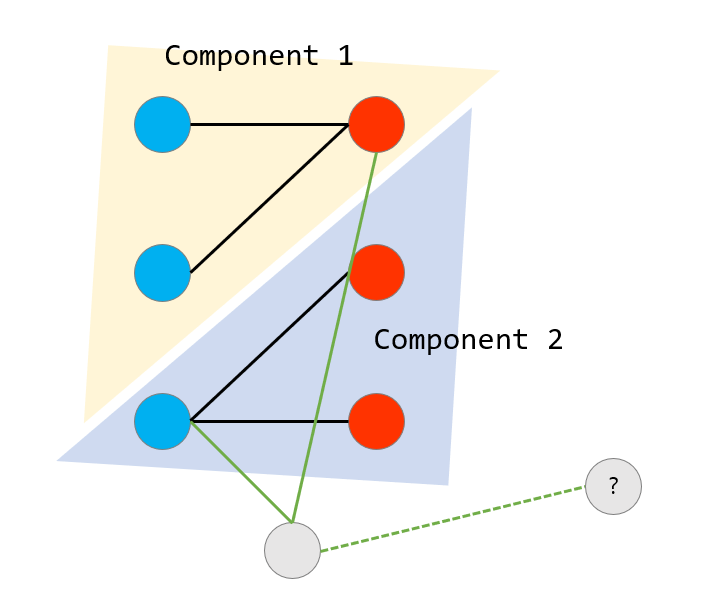
새로 정점 하나를 추가할 때 초록색 간선들이 달렸다고 생각해봅시다. 이때 각 컴포넌트는 이분 그래프가 맞지만, 임의로 지정한 색깔이 제대로 맞아들어가지 않습니다. 따라서 이런 경우 둘 중 하나의 컴포넌트를 골라 컴포넌트의 색을 통째로 뒤집어주어야 합니다. 이분 그래프는 보장이 되기 때문에 항상 잘 뒤집을 수 있습니다.
위 두 문제를 모두 해결하면 정답을 받을 수 있습니다.
Yet Another Interval Graph Problem (TST 2021 Day2 2번)
제거하는 원소의 가중치를 최소화하는 것은 사용하는 원소의 가중치를 최대화하는 것이라고 생각할 수 있고, 대부분 이 방향으로 생각하는 것이 구현하기 편합니다. 남겨놓는 원소의 가중치를 최대화하는 문제로 생각해봅시다.
Subtask 2 (17점)
$K = 1$이면 가중치 있는 회의실 배정 문제가 되고, 끝점 기준으로 정렬하고 DP를 하면 $O(N \log N)$ 혹은 $O(N^2)$시간에 해결할 수 있습니다. 회의실 배정 문제를 푼 뒤, 전체 가중치 합에서 뺀 값을 출력하면 됩니다.
Subtask 3 (0점)
Priority Queue 정렬 기준을 잘못 설정하면 이 서브태스크를 맞을 수 있습니다. 반성하면 됩니다.
Subtask 4 (36점, 총 53점)
$N \leq 250$인 걸 보니 $O(N^3)$ 정도에 풀어야 한다는 것을 예상할 수 있습니다.
정해로 발전할 수 없는 풀이와 발전할 수 있는 풀이가 존재합니다. 순서대로 설명하겠습니다.
Subtask 4 (1)
정해에 전혀 접근하지 못하는 풀이(그러나 처음 생각하기는 훨씬 쉬운 풀이) 입니다. 선분들을 시작점 순서대로 번호 붙이고, $DP[i][j][k]$를 $1$번부터 $i$번째 선분까지를 고려했을 때, 가장 오른쪽 컴포넌트에 포함된 간선 개수가 $j$이고 종료점이 가장 오른쪽에 있는 선분이 $k$번 선분일 때 삭제해야 하는 가중치 합의 최소라고 정의합시다. $i$의 범위는 $1\cdots N$, $j$의 범위는 $1\cdots K$, $k$의 범위는 $1\cdots N$이므로 고려해야 하는 상태의 수는 $O(N^3)$입니다.
그러면 $i$번 간선을 삭제할건지, 그렇지 않을 건지에 입각해서 상태 전이를 구성할 수 있습니다. 삭제한다면 $DP[i-1][j][k]$로부터 당겨올 수 있겠고, 그렇지 않다면 $DP[i-1][j-1][\text{max}]$로부터 당겨올 수 있겠습니다. 만약 $k$번 선분의 종료점보다 현재 선분의 시작점이 오른쪽에 있다면 공짜로 선분 하나를 남길 수 있다는 점까지 고려하면 각 상태 전이가 $O(1)$이므로 $O(N^3)$에 문제를 해결할 수 있습니다.
Subtask 4 (2)
끝점이 $i$ 이하인 선분들만 사용해서 만들 수 있는 가중치의 최댓값을 $D(i)$라고 정의합시다. 좌표 압축을 하면 $i$는 최대 $2N$입니다.
“끝점이 $i$ 이하인 선분들만 사용하는 것”은 $j < i$인 $j$에 대해 $D(j)$를 구성한 뒤, $(j, i]$ 구간에 완전히 포함되는 최대 $K$개의 선분을 선택하는 것과 동치입니다. 그러므로 $C(a,b)$를 $[a,b]$ 구간에 완전히 포함되는 최대 $K$개의 선분의 가중치 합의 최댓값이라고 정의하면, $D(i) = \max_{j < i}(D_j + C(j+1, i))$입니다.
$C(\ast,\ast)$는 $O(N^3)$에 모두 전처리할 수 있고, 점화식은 $O(N^2)$에 계산할 수 있으므로 전체 시간 복잡도는 $O(N^3)$입니다.
Subtask 5 (150점)
출제자가 왜 입력 제한을 $N \leq 5\,000$ 대신 $N \leq 2\,500$으로 정했을까요? $O(N^2)$ 뿐만 아니라 $O(N^2 \log N)$도 통과시키려는 의도라고 추측할 수 있습니다.
점화식을 계산하는 과정 자체는 이미 $O(N^2)$으로 충분히 빠르기 때문에, $C$를 전처리하는 과정을 최적화 해야 합니다. 고정된 $i$에 대해 $j$를 증가시키면서 $C(i, j)$를 구할 때, 선분이 추가되는 상황에서 가장 큰 $K$를 관리하는 작업은 min-heap을 이용해 수행할 수 있습니다. 즉, $C(i, j)$ 하나를 구할 때 $O(\log N)$이 걸리므로 $C(\ast,\ast)$를 모두 전처리하는 것은 $O(N^2 \log N)$ 시간에 할 수 있습니다.