두 번째 주의 AlgoShitPo에서 dual of a planar graph를 작성하게 된 ahgus89입니다.
평면 그래프(planar graph)
평면 그래프란, 이름처럼 평면 위에 놓여져 있는 그래프를 의미합니다. 정확히는, 적당한 평면이 존재하여 어떤 두 간선도 정점을 제외하고 교차하지 않는 그래프를 말합니다.
유명한 평면 그래프와, 그렇지 않은 것들의 예시로는 다음과 같은 것들이 있습니다.
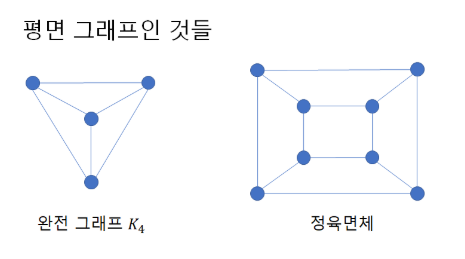
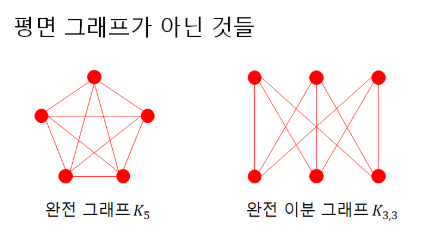
$K_5$나 $K_{3, 3}$을 minor로 가지는 것과 평면 그래프가 아님이 동치임이 알려져 있습니다.(Wagner’s theorem)
평면 그래프에서 성립하는 유명한 관계식이 몇 가지 있습니다.
단순 연결 평면 그래프가 $v \geq 3$개의 정점, $e$개의 간선, $f$개의 면을 가질 때 다음과 같은 관계식이 성립합니다.
- $e \leq 3v-6$
- 길이 3인 사이클(삼각형)이 없으면, $e \leq 2v-4$
- $f \leq 2v-4$
- $v-e+f=2$ (Euler characteristic)
이처럼 평면 그래프의 특수성 때문에 일반적인 그래프와는 다르게 $e = O(v)$가 성립합니다.
평면 그래프의 성질은 정말 다양한 것이 많지만, 이 글에서 다 다루지는 않겠습니다. 더 다양한 내용은 영문 위키에 잘 서술되어 있습니다.
듀얼 그래프(dual graph)
평면 그래프 $G$의 듀얼이란, $G$의 각 면을 정점으로 가지고, $G$의 간선으로 이웃한 두 면을 연결하는 간선을 가지는 그래프를 의미합니다. 앞서 설명한 평면 그래프의 듀얼은 다음과 같습니다.
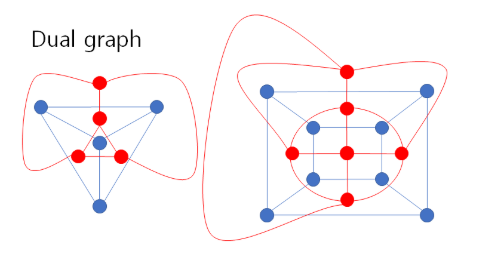
$G$의 듀얼 그래프는 $f$개의 정점, $e$개의 간선, $v$개의 면으로 이루어져 있으며 이 그래프의 듀얼은 다시 $G$가 됩니다. 듀얼 그래프는 위 그림처럼 multiple edge나 self-loop가 존재할 수 있지만, 역시 평면 그래프입니다. 또한, 모든 면이 간선을 통해 인접해 있으므로 항상 연결 그래프가 됩니다.
PS에서 유명한 dual 관계는 Voronoi diagram과 Delaunay triangulation이 있습니다.
듀얼 그래프 역시 더 많은 정보를 원한다면 영문 위키를 참조하시기 바랍니다. 문제풀이에 있어서는 듀얼의 개념만 알아도 충분합니다.
문제
이 문제를 풀어봅시다.
간단하게 요약하면, 평면 그래프와 $Q$개의 점이 주어지면 이전 점에서 현재 점으로 가는 최단 시간을 구하는 문제인데, 이때 그래프의 같은 면 내에서 이동할 때는 시간이 0, 간선으로 인접한 면으로 이동할 때는 $h_i$만큼의 시간이 듭니다.
생각
면에서 면으로의 이동은, 주어진 그래프의 듀얼 그래프에서 정점에서 정점으로의 이동으로 생각할 수 있습니다.
그렇기 때문에 듀얼 그래프에서 정점 사이의 최단거리들을 모두 전처리하고, 각 점이 듀얼 그래프의 어떤 정점에 속하는지 모두 구한다면 쿼리당 $O(1)$에 쉽게 처리할 수 있을 것입니다.
문제의 제한을 보면, $N-1 \leq M \leq N+100$이기 때문에, Euler characteristic을 생각해 보면 $f \leq 102$입니다. 따라서 듀얼 그래프만 구한다면 최단거리는 플로이드 워셜로 $O(f^3)$ 정도의 복잡도라도 충분함을 알 수 있습니다.
풀이를 우선 정리하면 다음과 같습니다.
- 주어진 평면 그래프의 듀얼 그래프를 만든다.
- 듀얼 그래프에서 플로이드 워셜로 최단거리 쌍을 모두 구한다.
- 쿼리로 주어진 점들이 듀얼 그래프에서 어떤 정점에 속하는지, 즉 원본 그래프의 어떤 면에 속하는지 구한다.
- 2와 3에서 구한 정보로 쿼리에 대한 답을 출력한다.
2와 4는 아주 간단하게 할 수 있고, 우리는 1과 3을 $200,000$ 정도의 제한 안에서 잘 해낼 방법을 찾아야 합니다.
듀얼 그래프 만들기
듀얼 그래프를 만드는 방법을 알아봅시다.
듀얼 그래프의 간선은, 원본 그래프의 간선의 양쪽에 있는 (같을 수도 있는)두 면을 연결합니다. 따라서 일단 $2e$개의 정점을 만들고, 같은 정점을 합쳐주는 방식으로 듀얼 그래프를 만들 수 있습니다.
예제를 예를 들어 설명하면, 우선 다음과 같은 그래프가 생깁니다.
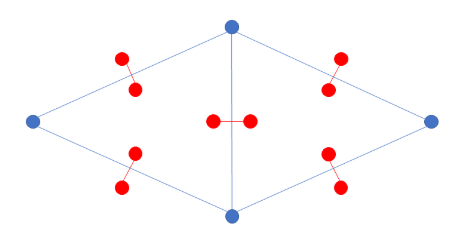
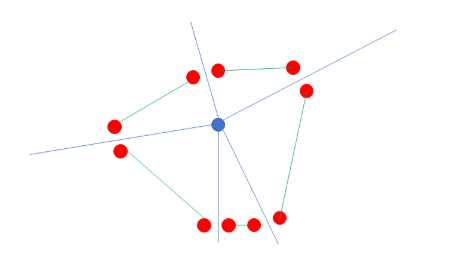
또한 한 점에 연결된 간선들만을 본다면, 아래 그림과 같이 연결된 정점들을 각도 순으로 정렬하면, 인접한 두 정점 사이의 영역은 유일하므로, 두 정점과 연결된 간선으로 나눠진 부분을 듀얼에서의 같은 정점으로 합쳐줄 수 있습니다.
정점을 합치는 과정은 Union-find로 구현할 수 있습니다.
따라서 듀얼 그래프를 만드는 과정의 시간 복잡도는, $N$개의 정점에 대해 각각 인접한 점들과 각도 정렬을 하고, Union-find로 합쳐주는 것만이 필요하므로, 총 $O(NlogN)$ 시간 안에 구할 수 있습니다.
한 점 기준으로의 각도 정렬, Union-find를 구현해야 하고, 그 외에도 합쳐줘야 할 점이 간선을 기준으로 어느 쪽인지 판별하기 쉽지 않아 구현이 까다로울 수 있습니다.
이때 외부에 해당하는 정점을 미리 구해두면 편리할 수 있습니다. $x$좌표가 가장 작은 정점에 대해 각도가 가장 큰 간선의 아래쪽이 외부에 해당하게 됩니다.
주어진 점이 듀얼 그래프의 어떤 정점에 속하는지 구하기
정점 $P_i (x_i, y_i)$에 대해, 직선 $x=x_i$와 교차하는 모든 선분들을 그 지점에서의 $y$좌표 순으로 정렬된 상태로 저장하고 있으면, lower_bound로 $P_i$ 위의 가장 가까운 선분을 구할 수 있고, 따라서 $P_i$는 그 선분의 아래쪽에 해당하는 영역에 포함됩니다.
$P_i$보다 위에 있는 선분이 없다면($x=x_i$와 교차하는 선분이 없는 경우 등), $P_i$는 외부 면에 해당하는 영역에 포함됩니다. 미리 구해둔 외부 영역을 알고 있기 때문에 쉽게 할 수 있습니다.
하지만 이 방법 그대로 구현하면, $O(NMlogM)$ 시간이 걸리게 됩니다.
시간복잡도를 줄이기 위해 주어진 점들을 모두 입력 받은 뒤, $x$축으로 sweeping 하면서 오프라인으로 처리해줄 수 있습니다.
주어진 그래프가 평면 그래프이기 때문에 교차하는 두 선분은 존재하지 않고, 그렇기 때문에 $x$좌표가 변화하더라도 $y$좌표의 크기 관계는 변화하지 않습니다.
따라서 std::set을 이용해, 원본 그래프의 정점이 주어진다면 그 정점과 연결된 간선에 대해 이미 set에 들어있는 간선은 지우고, 그렇지 않은 간선은 삽입하여 현재 $x$좌표를 지나는 선분들을 모두 $y$좌표 순으로 정렬하여 저장해 둘 수 있습니다. 이때 $y$축과 평행한 선분은 무시해줍니다.

이때 주의할 점이 있는데, 그 정점은 모든 선분이 교차하는 지점이므로, 선분이 $y$좌표 순으로 정렬이 되지 않습니다.
이미 존재하는 선분을 삭제할 때는 선분이 삽입될 때 $x$좌표가 현재보다 작았고, 새로 선분을 추가할 때는 앞으로 더 큰 $x$좌표에서 보게 될 것이므로, $x$좌표를 $(현재 x좌표-0.5)$로 둔 상태로 선분을 먼저 삭제한 뒤, $x$좌표를 $(현재 x좌표+0.5)$로 둔 상태로 선분을 추가하면 $y$좌표 순으로 정렬할 수 있습니다.
각 간선은 최대 한번씩만 넣고 빠지므로, 총 시간복잡도는 점 $x$좌표 순 정렬에 $O((Q+N)log(Q+N))$, 간선 삽입/삭제에 $O(MlogM)$, 쿼리 처리에 $O(QlogM)$의 시간에 해결할 수 있습니다. 따라서 전체 문제를 풀 수 있습니다.
정답 코드
#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef long long ll;
typedef pair<ll, ll> pii;
ll n, m, k, ans;
const ll mod=1e9+7;
pii p[202020], o;
ll h[202020], reg[202020];
vector<vector<pii>> graph(202020);
ll par[404040], out;
ll f(ll x){return x==par[x]?x:par[x]=f(par[x]);}
void uni(ll x, ll y){par[f(x)]=f(y);}
ll ccw(pii a, pii b, pii c)
{
ll ax=c.x-b.x, ay=c.y-b.y, bx=c.x-a.x, by=c.y-a.y, d=ax*by-ay*bx;
return (d>0)-(d<0);
}
bool cmp(pii a, pii b)
{
a=p[a.second], b=p[b.second];
if((a>o)^(b>o)) return a>b;
return ccw(a, o, b)>0;
}
ll dis[202][202];
double nx;
struct line{
double a, b;
ll i;
line(pii p, pii q, ll idx){
if(p>q) swap(p, q);
a=((double)(q.y-p.y))/(q.x-p.x);
b=p.y-a*p.x;
i=idx;
}
bool operator<(const line l) const{
if(a*nx+b!=l.a*nx+l.b) return a*nx+b<l.a*nx+l.b;
return i<l.i;
}
};
set<line> st;
bool vt[202020];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(0);
ll i, j, temp=0;
for(i=0;i<404040;i++)
par[i]=i;
cin>>n>>m;
for(i=1;i<=n;i++)
cin>>p[i].x>>p[i].y;
for(i=0;i<m;i++)
{
cin>>k>>j>>h[i];
graph[k].emplace_back(i, j);
graph[j].emplace_back(i, k);
}
for(i=1;i<=n;i++)
{
o=p[i];
sort(graph[i].begin(), graph[i].end(), cmp);//각도 정렬
ll u, v;
//간선의 어느쪽인지 판별
for(j=1;j<graph[i].size();j++)
{
u=2*graph[i][j-1].first+1, v=2*graph[i][j].first;
if(p[graph[i][j-1].second].x>o.x) u^=1;
if(p[graph[i][j-1].second].x==o.x&&p[graph[i][j-1].second].y<o.y) u^=1;
if(p[graph[i][j].second].x>o.x) v^=1;
if(p[graph[i][j].second].x==o.x&&p[graph[i][j].second].y<o.y) v^=1;
uni(u, v);
}
u=2*graph[i][j-1].first+1, v=2*graph[i][0].first;
if(p[graph[i][j-1].second].x>o.x) u^=1;
if(p[graph[i][j-1].second].x==o.x&&p[graph[i][j-1].second].y<o.y) u^=1;
if(p[graph[i][0].second].x>o.x) v^=1;
if(p[graph[i][0].second].x==o.x&&p[graph[i][0].second].y<o.y) v^=1;
uni(u, v);
}
i=min_element(p+1, p+n+1)-p;
out=f(2*graph[i][0].first+1);//외부
vector<pair<pii, ll>> q;
for(i=1;i<=n;i++)
q.emplace_back(p[i], i);
vector<ll> v;
for(i=0;i<m;i++)
{
v.push_back(f(2*i));
v.push_back(f(2*i+1));
}
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
n=v.size();
//플로이드
for(i=0;i<n;i++) for(j=0;j<n;j++) if(i!=j) dis[i][j]=1e18;
for(i=0;i<m;i++)
{
ll a=lower_bound(v.begin(), v.end(), f(2*i))-v.begin();
ll b=lower_bound(v.begin(), v.end(), f(2*i+1))-v.begin();
dis[a][b]=min(dis[a][b], h[i]);
dis[b][a]=min(dis[b][a], h[i]);
}
for(k=0;k<n;k++) for(i=0;i<n;i++) for(j=0;j<n;j++) dis[i][j]=min(dis[i][j], dis[i][k]+dis[k][j]);
cin>>m;
for(i=1;i<=m;i++)
{
cin>>j>>k;
q.emplace_back(pii(j, k), -i);
}
sort(q.begin(), q.end());
for(auto t:q)
{
nx=t.x.x;
if(t.second>0)
{
i=t.second;
nx-=0.5;//삭제 먼저
for(auto j:graph[i])
{
if(p[i].x==p[j.second].x) continue;
if(!vt[j.first]) continue;
line l(p[i], p[j.second], j.first);
st.erase(st.lower_bound(l));
}
nx+=1;//이후 삽입
for(auto j:graph[i])
{
if(p[i].x==p[j.second].x) continue;
if(vt[j.first]) continue;
line l(p[i], p[j.second], j.first);
vt[j.first]=1;
st.insert(l);
}
}
else
{
i=-t.second;
auto it=st.lower_bound(line(t.first, pii(mod, 0), 0));
if(it==st.end()) reg[i]=out;
else reg[i]=f(2*(it->i)+1);
reg[i]=lower_bound(v.begin(), v.end(), reg[i])-v.begin();
}
}
reg[0]=lower_bound(v.begin(), v.end(), out)-v.begin();
for(i=1;i<=m;i++)
cout<<dis[reg[i-1]][reg[i]]<<'\n';
}
제 구현 외에도 출제자의 코드 역시 한번 참고해 보시면 좋을 것 같습니다.
###연습 문제 BOJ 13145 Masonry Bridge
풀이의 방향
연결 시간의 최솟값과 최댓값을 구하는 문제인데, 최솟값의 경우 다익스트라로 쉽게 구할 수 있습니다.
최댓값이 문제인데, 듀얼 그래프를 생각해봅시다. 이때, 직선 $x=x_1$과 $x=x_N$을 추가로 그어 가장 바깥쪽 영역을 위와 아래로 나누어 줍니다. $1$번 점과 $N$번 점은 각각 $x$좌표가 최소, 최대이므로 이렇게 나눌 수 있습니다.
듀얼 그래프의 간선 중 원본 그래프에서 연결되지 않은 간선만을 포함하는 그래프를 생각하면, $1$번 점과 $N$번 점이 연결되기 직전에는, 위에서 나눈 ‘위’와 ‘아래’ 영역을 그 그래프의 간선만으로 이동할 수 있고, 연결되는 순간부터는 이동할 수 없습니다.
마지막으로 연결된 간선이 듀얼 그래프의 정점 $A$와 $B$를 연결한다면, 소요 시간은 $(모든 \space 간선 \space 가중치의 \space 합)-(“위”에서 \space A까지의 \space 최단 \space 거리)-(B에서 \space “아래”\space 까지의 \space 최단 \space 거리)$가 됩니다. $1$번 정점과 $N$번 정점에서 다익스트라 알고리즘으로 최단거리를 구해 이 값 또한 구해낼 수 있습니다.
$M \leq 10^6$이라는 제한이 빡세 보일 수 있지만, 위에서 언급한 평면 그래프의 성질 때문에 실제로 $M \leq 150000$ 정도입니다.